- GitHub 1-3 : GraphQL, PostgreSQL, programmation fonctionnelle, L-systems
- GitHub 4-6 : system design, collection O RLY, graphisme geek
Lorsqu’on connaît les valeurs que prend une fonction seulement en certains points et qu’on souhaite lui attribuer une valeur en d’autres points, on peut effectuer ce qu’on appelle une interpolation.
Si l’on souhaite avoir une interpolation plutôt lisse, il est possible d’utiliser des splines, qui sont des fonctions polynomiales par morceau. Dans ce billet, on s’intéresse au cas particulier des splines cubiques de Hermite, basées sur les polynômes de Hermite.
Exemple
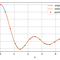
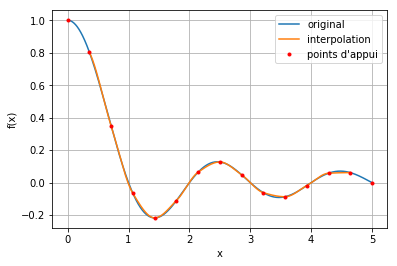
Voici un exemple pour la fonction sinus cardinal sur l’intervale [0,9].
Définition
On dispose d’un ensemble de points , …, , rangés par ordre croissant, pour lesquels on connaît la valeur que prend la fonction . Autrement dit, on connaît les valeurs , …, .
L’interpolation cubique de Hermite attribue à la fonction sur chaque intervalle les valeurs prises par un polynôme de Hermite d’ordre 3 :
où et sont les dérivées aux points et respectivement. Ce sont des paramètres à déterminer (voir plus loin).
Les dérivées ne sont pas disponibles dans les données du problème, elles sont donc estimées à partir de celles-ci.
On note les écarts :
Pour un point , on définit la dérivée à gauche par :
et la dérivée à droite par :
Si les dérivées à droite ou à gauche sont de signes opposés ou une des deux est nulle, alors . On force en fait un extremum local ou un plateau. Autrement, la dérivée est alors prise comme la moyenne harmonique des dérivées à gauche et à droite :
avec et , qui sont des coefficients permettant de prendre en compte la répartition inégale des .
Les points aux limites nécessitent un traitement particulier non abordé ici.
Implémentation en Python
Une implémentation rudimentaire en Python se trouve ci-dessous.
import numpy as np
import matplotlib.pyplot as plt
# # Test Function
xmin = 0
xmax = 5
def testFun(x):
return np.sin(x)*np.exp(-0.5*x)
def testFun(x):
return np.sinc(x)
# ## High Resolution
xinf = np.linspace(xmin, xmax, 1001)
yinf = testFun(xinf)
# ## Samples
x = np.linspace(xmin, xmax, 15)
y = testFun(x)
# # Tools for the Examples
def plot(x0, y0, x, y, xinf, yinf):
plt.plot(xinf,yinf, label='original')
plt.plot(x0, y0, label='interpolation')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x,y,'r.', label='points d\'appui')
plt.grid()
plt.legend()
plt.show()
def evaluateAt(x0, f):
y0 = np.zeros(len(x0))
for i in range(len(x0)):
y0[i] = f(x0[i])
return y0;
# # Cubic Hermite Interpolation
def interpolant3(x, y):
def interpFn(xx):
if xx <= x[1] or xx > x[-2]:
return float('nan')
else:
i2 = 0
while xx > x[i2]:
i2 += 1
i1 = i2 - 1
i0 = i1 - 1;
i3 = i2 + 1;
x0 = x[i0]
x1 = x[i1]
x2 = x[i2]
x3 = x[i3]
y0 = y[i0]
y1 = y[i1]
y2 = y[i2]
y3 = y[i3]
d0 = (y1 - y0)/(x1-x0)
h0 = (x1-x0)
d1 = (y2 - y1)/(x2-x1)
h1 = (x2-x1)
d2 = (y3 - y2)/(x3-x2)
h2 = (x3-x2)
if d0*d1 > 0:
w01 = h0 + 2*h1
w11 = h1 + 2*h0
m1 = (w01 + w11)/(w01/d0 + w11/d1)
else:
m1 = 0
if d1*d2 > 0:
w02 = h1 + 2*h2
w12 = h2 + 2*h1
m2 = (w02 + w12)/(w02/d1 + w12/d2)
else:
m2 = 0
p1 = y1
p2 = y2
t = (xx - x1)/(x2 - x1)
res1 = (2*(t**3)-3*(t**2) + 1)*p1
res2 = (t**3 - 2*(t**2) + t)*(x2 - x1)*m1
res3 = (-2*(t**3) + 3*(t**2) )*p2
res4 = ((t**3) - (t**2))*(x2 - x1)*m2
res = res1 + res2 + res3 + res4
return res
return interpFn
f3 = interpolant3(x, y)
x0 = np.linspace(xmin, xmax, 10001)
y0 = evaluateAt(x0, f3)
plot(x0, y0, x, y, xinf, yinf)
Discussion
Avantages
L’interpolation est lisse (classe C1 pour être précis).
La forme des données est préservée, c’est-à-dire que la fonction est monotone sur chaque intervalle.
Inconvénients
Les calculs sont plus lourds que pour les interpolations plus simples.
La dérivée seconde n’est pas continue, ce qui peut poser problème.
Quand l’utiliser ?
Dès qu’il est nécessaire d’avoir une fonction d’interpolation de classe C1. Si la fonction doit être encore plus lisse, il faut passer aux splines cubiques naturelles, mais on perd la préservation de la forme.