« Quel est ton algorithme préféré ? »
Elle a l’air un peu idiote cette question, et pourtant j’avais un collègue qui la posait systématiquement aux candidats en entretien d’embauche. Une petite question ouverte sympa, qui permet de détendre l’atmosphère et d’en apprendre beaucoup sur un potentiel futur collègue.
À bien y réfléchir, ma propre réponse à cette question a pas mal évolué au cours de ma carrière. Si l’on me la posait aujourd’hui, je pense que je répondrais sans hésiter l’algorithme de recherche de motifs d’Aho-Corasick, parce que cet algo est simple et pourtant capable de faire des miracles dans une foultitude de situations différentes, pour peu qu’on ait assez d’imagination pour penser à lui.
Cet algorithme sert à rechercher toutes les occurrences d’un nombre arbitraire de motifs (ou mots-clés) dans un flux d’information (un texte), avec une complexité qui ne dépend que de la longueur du texte. Cela veut dire non seulement que la recherche est tout aussi efficace, qu’elle porte sur une dizaine ou plusieurs centaines de motifs distincts, mais également que la complexité algorithmique de cette recherche est optimale.
Initialement formulé par Alfred Aho et Margaret Corasick durant les années 19701, l’algorithme en lui-même consiste à construire un automate fini déterministe (AFD) que l’on évalue en parcourant le flux d’entrée. Depuis une dizaine d’années, on le retrouve cité en référence de nombreux papiers qui cherchent à rendre pratiquable sa généralisation à des expressions régulières (plutôt de que des mots-clés).
-
Alfred V. Aho et Margaret J. Corasick, juin 1975, Efficient string matching: An aid to bibliographic search, Communications of the ACM, vol. 18, issue 6, pages 333–340 ↩
Le module acora
Plutôt que de nous attarder sur l’aspect théorique de cet algo, jouons plutôt avec une implémentation qui fonctionne. Si vous tenez à étudier les tenants et les aboutissants de la création d’un AFD, je vous renvoie vers la page wikipédia et l’article originel, dans lesquels vous trouverez toutes les infos dont vous aurez besoin.
En Python, celui-ci est implémenté avec des performances remarquables dans le
module acora, disponible dans le PyPI :
1 | pip3 install acora |
L’utiliser est un jeu d’enfants :
1 2 3 4 5 | >>> data = "Le grigri gris du gros grison est grisant" >>> builder = AcoraBuilder(("gris", "gros", "gras")) >>> matcher = builder.build() >>> matcher.findall(data) [('gris', 10), ('gros', 18), ('gris', 23), ('gris', 34)] |
En somme, le module s’utilise en deux temps : d’abord on construit une machine
de recherche, et ensuite on l’utilise sur les données d’entrée. Il est
important de noter qu’une machine, une fois construite, peut être sérialisée
avec le module pickle pour vous épargner la compilation de l’automate à
chaque utilisation.
Le résultat d’une recherche se présentera toujours sous la forme d’une séquence
(liste dans le cas de findall(), générateur dans le cas de finditer()) de
paires (mot-clé, position), qui indiquent la position les motifs trouvés dans
la chaîne.
Par exemple, voici un script qui va compter le nombre d’occurrences des noms des personnages principaux du premier tome des Misérables de Victor Hugo :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | #!/usr/bin/env python3 from acora import AcoraBuilder from collections import Counter FILENAME = 'les_miserables_tome_1.txt' KEYWORDS = ('Valjean', 'Fantine', 'Javert', 'Thénardier', 'Cosette') MATCHER = AcoraBuilder(KEYWORDS).build() def main(): with open(FILENAME) as book: data = book.read() count = Counter(kwd for kwd, _ in MATCHER.findall(data)) for kwd, occurs in count.items(): print('{}: {} occurrences'.format(kwd, occurs)) if __name__ == '__main__': main() |
Et voici sa sortie :
1 2 3 4 5 | Thénardier: 57 occurrences Cosette: 61 occurrences Javert: 177 occurrences Valjean: 197 occurrences Fantine: 191 occurrences |
Benchmarkons, les amis, benchmarkons
Pour bien nous rendre compte des performances de cet algorithme, réalisons
un petit benchmark en le mettant face à face avec le module standard re de
Python.
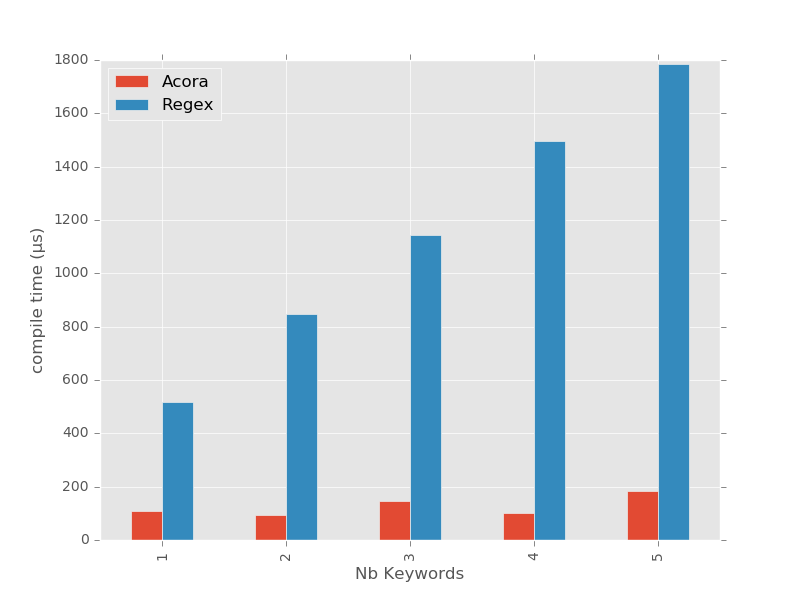
Nous allons comparer le temps de compilation d’une machine Aho-Corasick avec celui de l’expression régulière équivalente, en utilisant les deux fonctions suivantes :
1 2 3 4 5 6 7 8 9 10 11 | KEYWORDS = ('Valjean', 'Fantine', 'Javert', 'Thénardier', 'Cosette') def compile_regex(n_keys): return re.compile( '|'.join(key for key, _ in zip(KEYWORDS, range(n_keys))) ) def compile_matcher(n_keys): return AcoraBuilder( tuple(key for key, _ in zip(KEYWORDS, range(n_keys))) ).build() |
Les deux fonctions prennent en argument le nombre de mots-clés que nous désirons compter dans le texte. Les fonctions réalisant le comptage sont les suivantes :
1 2 3 4 5 6 7 8 9 10 | def count_regex(regex, data): return Counter( regex.findall(data) ) def count_acora(matcher, data): return Counter( kwd for kwd, _ in matcher.findall(data) ) |
Voici le résultat, mesuré grâce au module
line_profiler :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | Timer unit: 1e-06 s
Total time: 5.72198 s
File: aho_corasick.py
Function: main at line 30
Line # Hits Time Per Hit % Time Line Contents
==============================================================
30 @profile
31 def main():
32 1 56 56.0 0.0 with open(FILENAME) as book:
33 1 5083 5083.0 0.1 data = book.read()
34
35 1 518 518.0 0.0 regex_1_key = compile_regex(1)
36 1 847 847.0 0.0 regex_2_keys = compile_regex(2)
37 1 1142 1142.0 0.0 regex_3_keys = compile_regex(3)
38 1 1497 1497.0 0.0 regex_4_keys = compile_regex(4)
39 1 1786 1786.0 0.0 regex_5_keys = compile_regex(5)
40
41 1 109 109.0 0.0 matcher_1_key = compile_matcher(1)
42 1 94 94.0 0.0 matcher_2_keys = compile_matcher(2)
43 1 147 147.0 0.0 matcher_4_keys = compile_matcher(4)
44 1 102 102.0 0.0 matcher_3_keys = compile_matcher(3)
45 1 184 184.0 0.0 matcher_5_keys = compile_matcher(5)
46
47
48 101 157 1.6 0.0 for _ in range(100):
49 100 67666 676.7 1.2 count_regex(regex_1_key, data)
50 100 1016259 10162.6 17.8 count_regex(regex_2_keys, data)
51 100 772214 7722.1 13.5 count_regex(regex_3_keys, data)
52 100 776246 7762.5 13.6 count_regex(regex_4_keys, data)
53 100 787416 7874.2 13.8 count_regex(regex_5_keys, data)
54
55 100 440147 4401.5 7.7 count_acora(matcher_1_key, data)
56 100 450821 4508.2 7.9 count_acora(matcher_2_keys, data)
57 100 462348 4623.5 8.1 count_acora(matcher_3_keys, data)
58 100 465644 4656.4 8.1 count_acora(matcher_4_keys, data)
59 100 471496 4715.0 8.2 count_acora(matcher_5_keys, data)
|
On se rend compte que le temps de compilation des expressions régulières est proportionnel au nombre de mots-clés, là où celui de la machine Aho-Corasick reste stable.
Le temps d’exécution de la recherche, quant à lui, est un peu plus rigolo à interpréter.
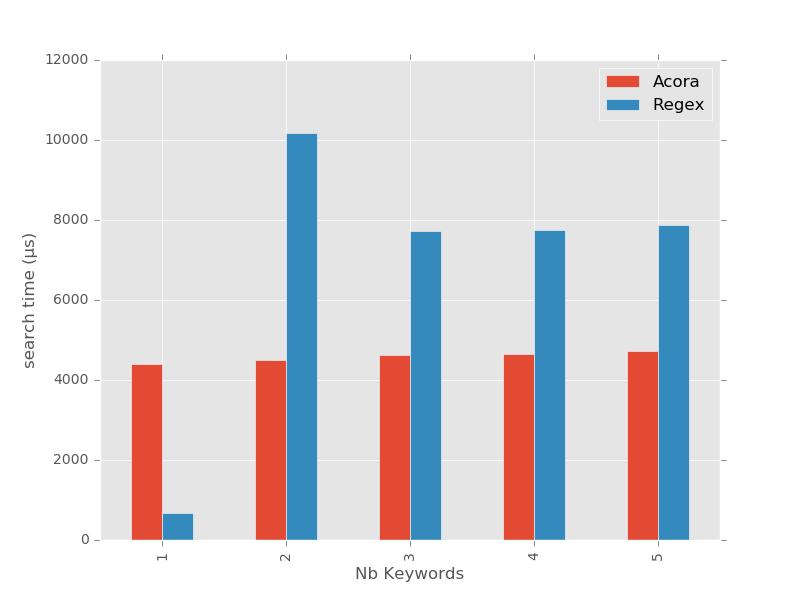
D’abord, commençons par le plus facile : on peut remarquer que le moduleacora reste, comme promis, tout à fait stable quel que soit le nombre de
mots-clés. On s’aperçoit que la recherche des mots-clés est du même ordre de
grandeur que le chargement de la totalité du livre (694 Ko) en mémoire, soit aux
alentours de 5ms.
Les résultats du module re, par contre, sont plutôt intéressants, parce
qu’ils nous donnent une bonne indication sur la façon dont Python optimise ses
expressions régulières.
D’abord, lorsque l’on ne recherche qu’un seul mot-clé ("Valjean"), on
s’aperçoit que le comptage est bigrement rapide ! En fait, dans le cas précis
où la recherche porte sur une simple sous-chaîne de caractères, le module re
se rappatrie sur l’algorithme de recherche natif des chaînes de Python, qui se
base grosso-modo sur la méthode deBoyer-Moore.
Ensuite, curieusement, lorsque la recherche porte sur deux mots-clés
("Valjean|Fantine"), le module re ne semble absolument pas optimiser sa
recherche, et compiler une expression rationnelle "générique" (un
automate fini non-déterministe, ou AFN), ce qui explique que le chrono explose
par rapport à l’AFD du module acora.
Enfin, et c’est là que c’est le plus rigolo, à partir de 3 mots-clés, le modulere optimise son pattern en générant justement un AFD à-la-Aho-Corasick, ce
qui explique qu’il reste stable aux environs de 7ms sur les 3 dernières
recherches. On notera toutefois que l’implémentation, tout comme la
compilation, restent plus lentes que celles, explicites et spécialisées dans
ce type de recherche, du module acora.
Essayons de compliquer encore un peu la donne en réalisant des recherches insensibles à la casse :
1 2 3 4 5 6 7 8 9 10 | def compile_regex(n_keys): return re.compile( '|'.join(key for key, _ in zip(KEYWORDS, range(n_keys))), re.IGNORECASE ) def compile_matcher(n_keys): return AcoraBuilder( tuple(key for key, _ in zip(KEYWORDS, range(n_keys))) ).build(ignore_case=True) |
Si les temps de compilation ne bougent pas trop, on remarque que les temps de recherche, eux, ne sont plus du tout les mêmes :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | Timer unit: 1e-06 s
Total time: 29.6532 s
File: aho_corasick.py
Function: main at line 31
Line # Hits Time Per Hit % Time Line Contents
==============================================================
31 @profile
32 def main():
33 1 54 54.0 0.0 with open(FILENAME) as book:
34 1 4632 4632.0 0.0 data = book.read()
35
36 1 478 478.0 0.0 regex_1_key = compile_regex(1)
37 1 780 780.0 0.0 regex_2_keys = compile_regex(2)
38 1 1015 1015.0 0.0 regex_3_keys = compile_regex(3)
39 1 1405 1405.0 0.0 regex_4_keys = compile_regex(4)
40 1 1724 1724.0 0.0 regex_5_keys = compile_regex(5)
41
42 1 140 140.0 0.0 matcher_1_key = compile_matcher(1)
43 1 136 136.0 0.0 matcher_2_keys = compile_matcher(2)
44 1 255 255.0 0.0 matcher_4_keys = compile_matcher(4)
45 1 174 174.0 0.0 matcher_3_keys = compile_matcher(3)
46 1 334 334.0 0.0 matcher_5_keys = compile_matcher(5)
47
48
49 101 206 2.0 0.0 for _ in range(100):
50 100 1216017 12160.2 4.1 count_regex(regex_1_key, data)
51 100 3607006 36070.1 12.2 count_regex(regex_2_keys, data)
52 100 5060056 50600.6 17.1 count_regex(regex_3_keys, data)
53 100 6607653 66076.5 22.3 count_regex(regex_4_keys, data)
54 100 8019853 80198.5 27.0 count_regex(regex_5_keys, data)
55
56 100 670430 6704.3 2.3 count_acora(matcher_1_key, data)
57 100 936639 9366.4 3.2 count_acora(matcher_2_keys, data)
58 100 1094195 10942.0 3.7 count_acora(matcher_3_keys, data)
59 100 1217311 12173.1 4.1 count_acora(matcher_4_keys, data)
60 100 1212728 12127.3 4.1 count_acora(matcher_5_keys, data)
|
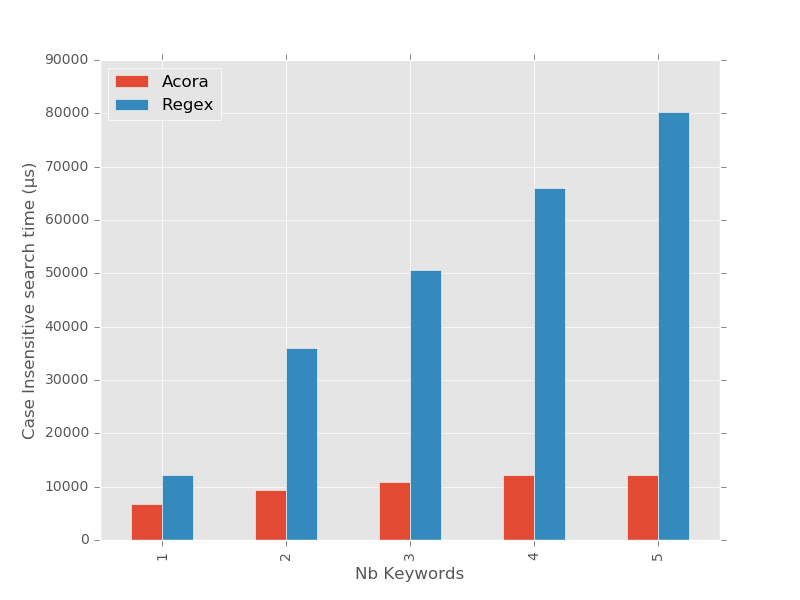
Clairement, ce qui frappe en premier, c’est que le module standard re ne sait
plus optimiser les expressions rationnelles à partir du moment où l’on lui
demande de devenir insensible à la casse. Les temps de recherche redeviennent
proportionnels au nombre de mots-clés recherchés.
L’autre remarque que l’on peut faire, c’est que si l’insensibilité à la
casse divise les performances de sa recherche par 2 ou 3, les temps d’acora
restent stables aux alentours de 10ms : les deux algos de recherche ne jouent
plus du tout dans la même cour.
Ce qu’il faut retenir, c’est que le premier critère grâce auquel le module
acora est l’un de mes préférés, c’est d’abord le fait qu’il envoie du pâté
question performances : pour une même quantité de données en entrée, le
temps de calcul de la recherche sera toujours le même, quel que soit le nombre
de mots-clés recherchés, donc c’est l’algorithme optimal pour chercher toutes
les occurrences d’un (très) grand nombre de mots-clés dans un flux
d’informations.


