À partir d’un certain âge, tout le monde (ou presque) sait s’habiller dans le bon ordre. Il y a même plusieurs ordres possibles ! Ainsi, on peut tout à fait enfiler ses chaussettes avant son maillot de corps ou l’inverse. D’autres vêtements ne peuvent pas être inversés : on doit par exemple mettre ses chaussettes avant ses chaussures. Comme on sait que tel vêtement devrait venir avant tel autre, on sait dire que l’ordre « maillot de corps, puis chaussettes, puis chaussures » est correct, alors que « chaussures, puis t-shirt, puis chaussettes » ne l’est pas.
Quand le nombre de vêtement augmente, cela se complique. Comment savoir facilement si un ordre d’habillage quelconque est correct ? Et comment trouver un bon ordre de manière systématique à partir d’une liste de vêtements ?
On pourrait évidemment se contenter de la sagesse populaire pour répondre à ces questions, comme on le fait tous les jours, mais ce ne serait pas amusant. Cet article propose de répondre à ses questions mathématiquement. C’est parti !
Cet article est accessible à toute personne avec le bagage mathématique du secondaire.
Ordre partiel de l'habillage
Ordre partiel des vêtements
Commençons par quelques observations sur l’ordre dans lequel les vêtements doivent s’enfiler.
- On sait que parfois un vêtement doit nécessairement venir avant un autre, l’inverse étant impossible. Le caleçon doit être mis avant le pantalon ; on ne peut pas le faire dans l’autre sens.1
- D’autres fois, le sens ne compte pas. Par exemple, maillot de corps et chaussettes peuvent être inversés sans problème ; il n’y a pas de relation particulière entre les deux.
Ces deux observations indiquent que l’ordre d’habillage correspond à ce qu’on appelle en mathématique un ordre partiel strict. Autrement dit, il s’agit d’une relation où on peut comparer certains éléments deux à deux, mais pas tous.
Pour être sûr qu’il s’agit bien d’un ordre partiel, nous devons cependant vérifier qu’il en a bien toutes les propriétés : il doit être antisymétrique et transitif.
L’antisymétrie est une propriété au nom compliqué mais en vérité toute simple : si un vêtement A doit être enfilé avant un vêtement B, alors on n’a pas l’inverse (le vêtement B avant le vêtement A). C’est assez évident pour l’ordre d’enfilage des vêtements, pas besoin de s’étendre dessus.
Être transitif signifie qu’il est possible de faire des chaînes de comparaisons : si un vêtement A doit être enfilé avant un vêtement B et un vêtement B avant un vêtement C, alors le vêtement A doit être enfilé avant le vêtement C. C’est assez simple de se convaincre que c’est le cas sur un exemple : si on a un maillot de corps à enfiler avant un t-shirt et un t-shirt à mettre avant un pull, alors il faut enfiler le maillot de corps avant le pull.
En fait, on parle d’ordre partiel par opposition à l’ordre total. L’ordre total est celui dont on a l’habitude avec les nombres. En effet, de deux nombres, on sait toujours lequel arrive avant l’autre ; on n’a jamais de cas où on ne peut pas donner la réponse. L’ensemble des nombres est donc totalement ordonné. L’ensemble des vêtements ne l’est que partiellement !
Exemple
Faisons un exemple pour illustrer tout ça. Pour ajouter un peu de réalisme, travaillons sur un exemple avec un nombre assez important de vêtements : chaussures, chaussettes, pantalon, caleçon, maillot de corps, t-shirt, pull.
Pour chaque vêtement, il est possible de le comparer à tous les autres, on saura à chaque fois s’il est avant, s’il est après, si on ne peut pas donner d’ordre (symbole « ? »), ou si la comparaison n’a pas lieu d’être (symbole « - »). Ce travail est facile mais long, aussi je donne directement les résultats de ces comparaisons dans le tableau ci-dessous. Il faut le lire ligne par ligne. Par exemple, la première ligne dit « Chaussures après chaussettes », « Chaussures après pantalon », etc.
| Chaussures | Chaussettes | Pantalon | Caleçon | Maillot de corps | T-shirt | Pull | |
|---|---|---|---|---|---|---|---|
| Chaussures | - | Après | Après | Après | ? | ? | ? |
| Chaussettes | Avant | - | ? | ? | ? | ? | ? |
| Pantalon | Avant | ? | - | Après | ? | ? | ? |
| Caleçon | Avant | ? | Avant | - | ? | ? | ? |
| Maillot de corps | ? | ? | ? | ? | - | Avant | Avant |
| T-shirt | ? | ? | ? | ? | Après | - | Avant |
| Pull | ? | ? | ? | ? | Après | Après | - |
Regardez bien ce tableau : quand on compare les éléments symétriques par rapport à la diagonale, on voit que si on a « avant », alors on aura « après » dans l’autre case et que si on a un « ? » alors la case symétrique aura aussi un « ? ». C’est exactement la signification de l’antisymétrie : quand on effectue la symétrie, la relation est inversée !
Même si c’est bien moins visuel, on peut aussi vérifier les relations de transitivité. Par exemple, le maillot de corps est avant le t-shirt et le t-shirt est avant le pull, et on a bien que le maillot de corps est avant le pull.
Ce tableau est utile pour stocker l’information, mais pas pour la présenter. Il faut trouver mieux !
- Sauf Superman, mais pour les besoins de l’article, supposons qu’il reste Clark Kent.
↩
Graphe de l'habillage
Graphe de l’habillage
Nous avons vu que nous avions donc d’un côté des vêtements et de l’autre côté des relations entre eux, du type « vêtement A avant vêtement B ». Ces deux facettes peuvent être représentées à l’aide d’un graphe.
Pour faire simple, un graphe est un ensemble d’objets, appelés des nœuds, reliés entre eux par des flèches, qu’on appelle des arêtes. Dans notre cas, les nœuds seront les vêtements et les flèches seront les relations. La direction de la flèche est importante : quand le vêtement A est avant le vêtement B, elle partira de A pour arriver à B.
Il n’y a pas besoin de représenter les relations « après », parce que l’information est en vérité déjà contenue dans la flèche « avant » : il suffit de la prendre en sens inverse. L’absence d’information correspond à l’absence d’arête.
Le diagramme ci-dessous montre le graphe obtenu à partir du tableau de la section précédente.

Simplification du graphe par transitivité
Le graphe contient toute l’information nécessaire pour travailler dessus, mais il contient des redondances. Heureusement, il est facile de le simplifier.
Souvenez-vous : l’ordre partiel des vêtements est transitif. Cela signifie qu’à chaque fois qu’on a la structure suivante :
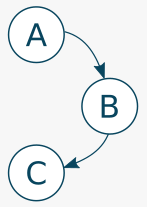
On peut en déduire celle-ci :
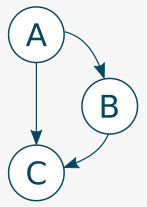
Autrement dit, on peut simplifier le graphe en ne gardant que la première structure, puisque la deuxième structure est seulement une conséquence de la première.
On obtient le résultat suivant.
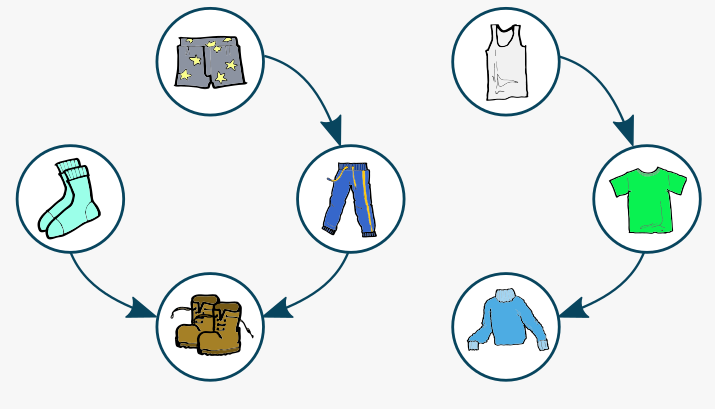
Maintenant que nous avons notre graphe, il est possible d’utiliser tous les algorithmes de graphe connus dessus !
Trouver le bon ordre avec un tri topologique
Tri topologique
Le graphe simplifié contient la totalité de l’information sur l’interdépendance entre les vêtements, il doit donc être possible d’en tirer une séquence qui respecte les contraintes de l’habillage. Une telle séquence s’appelle un tri topologique, et des algorithmes de graphe résolvant cette tâche existent.
Un tri topologique n’est rien d’autre qu’une liste ordonnée des vêtements présents dans le graphe, telle que si un vêtement est avant un autre dans le graphe, alors soit il n’a pas d’arête vers aucun d’eux, ou alors ces arêtes montrent que ce vêtement doit être avant.
Voici un exemple de tri topologique de notre graphe : chaussettes, maillot de corps, caleçon, t-shirt, pantalon, chaussures, pull.
Un tri topologique s’appelle ainsi, parce qu’il respecte la forme du graphe, qu’on appelle aussi sa topologie.
Trouver un tri topologique
Il existe différents algorithme pour obtenir un tri topologique d’un graphe. Nous nous intéressons dans cet article à l'algorithme de Kahn. Je ne procéderai pas à la description détaillée de l’algorithme, mais expliquerai seulement ses principes généraux puis effectuerai une démonstration sur notre exemple.
L’algorithme procède comme suit.
- Lister les vêtements qu’on peut enfiler tout de suite (ceux sans arête qui pointe vers eux).
- En prendre un et l’enfiler.
- Supprimer les relations désormais satisfaites (donc les arêtes qui viennent du vêtement qu’on vient d’enfiler).
- Mettre à jour la liste des vêtements qu’on peut enfiler toute de suite (ceux n’ayant plus aucune arrête pointant vers eux).
- Reprendre au point 2. ou s’arrêter quand tous les vêtements sont enfilés.
Faisons le fonctionner pas à pas sur notre exemple. Notez que je prends le graphe simplifié, mais que l’algorithme marche tout aussi bien sur le graphe d’origine.

Étape 1 : Au départ, on peut enfiler les vêtements suivants : caleçon, maillot de corps ou chaussettes. Enfilons le caleçon. En faisant cela, le caleçon disparaît du graphe, ainsi que l’arête qui pointe vers le pantalon. Le pantalon n’a plus d’arêtes, on l’ajoute à la liste des vêtements que l’on peut enfiler. Vêtements enfilés : caleçon.
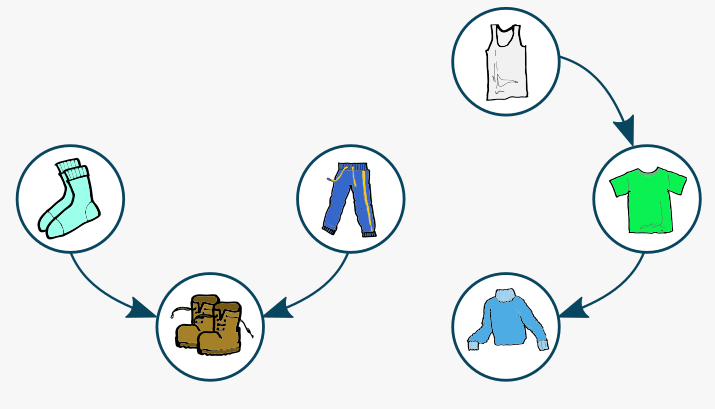
Étape 2 : La liste des vêtements qu’on peut enfiler est la suivante : maillot de corps, chaussettes, pantalon. On en enfile un, disons le pantalon. On peut enlever du graphe le pantalon et l’arête vers les chaussures. Vêtements enfilés : caleçon, puis pantalon.
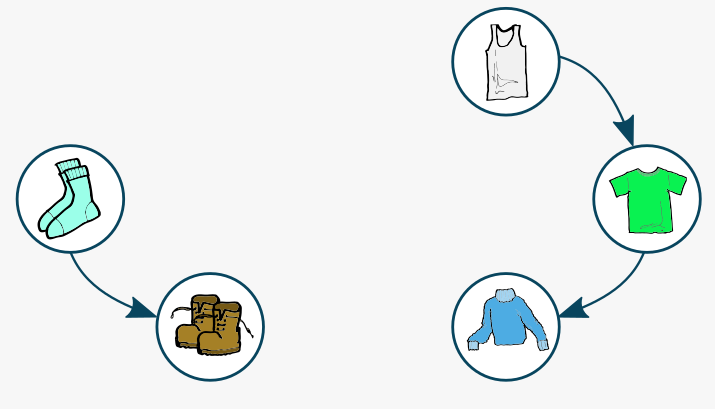
Étape 3 : La liste de vêtements qu’on peut enfiler est : maillot de corps, chaussettes. On enfile les chaussettes, on met à jour le graphe en supprimant les chaussettes et l’arête associée. Vêtements enfilés : caleçon, puis pantalon, puis chaussettes.
Étapes 4, 5, 6, 7 : On continue ainsi et on enfile chaussures, puis maillot de corps, puis t-shirt puis pull. La liste est alors vide. On obtient finalement l’ordre suivant : caleçon, puis pantalon, puis chaussettes, puis chaussures, puis maillot de corps, puis t-shirt, puis pull !
Vous constaterez que le tri obtenu n’est pas le même que celui donné en exemple au début de cette partie. En effet, il y a en général plusieurs tris topologiques possibles pour un même graphe. Ils correspondent dans notre cas à l’ordre de choix des vêtements lorsque que plusieurs vêtements peuvent être enfilés à la même étape.
Un tri topologique consiste à établir un ordre total à partir d’un ordre partiel ! Dans le graphe, on ne sait pas toujours si un vêtement est avant ou après l’autre. En construisant une liste lors d’un tri topologique, on fait un choix sur qui vient avant. Une fois fini, le tri permet de dire pour toute paire de vêtement lequel est enfilé avant l’autre ou inversement : on a un ordre total.
Le lien entre les ordres et les graphes est en fait assez profond. La théorie mathématique qui justifie rigoureusement cette relation étroite est celle des foncteurs adjoints.
Voilà ! Vous savez désormais enfiler vos vêtements mathématiquement dans le bon ordre. Au-delà de cette connaissance très spécifique, vous avez pu voir comment les mathématiques permettent de modéliser le monde réel (celui de vêtements) pour résoudre efficacement un problème.
De l’habillage des vêtements, nous sommes passés à une formulation mathématique en termes de relations d’ordre. Nous avons pu ensuite représenter ces relations sous forme de graphe, un changement de cadre ouvrant tous outils de la théorie des graphes et facilitant la résolution du problème.
Au passage, vous avez observé comment des liens se font naturellement entre les différents domaines des mathématiques, dans notre cas les ordres et les graphes. D’un ordre partiel, on tire un graphe, puis du tri topologique d’un graphe, on revient à la théorie initiale en formant un ordre total. Tisser de tels liens est d’ailleurs une activité que les mathématiciens apprécient, et ce d’autant plus que les liens paraissent forts ou insoupçonnés.
Si le problème de l’habillage vous a paru simpliste, sachez que de nombreux problèmes plus complexes sont apparentés à celui-là et impliquent des relations d’ordre et des algorithmes de graphes. On peut citer notamment la planification de tâches (dans quel ordre réaliser des tâches interdépendantes pour mener à bien un projet ?) et la résolution de dépendances logicielles (dans quel ordre installer des logiciels qui dépendent les uns des autres ?)
Les cliparts de vêtements sont sous licence CC-0 (source).