Vous avez surement déjà entendu parler du deep learning ! Cette technologie est devenue populaire depuis quelques années et on en entend parler de plus en plus souvent dans la presse généraliste. Dans cet article nous allons avoir un aperçu de ce qu’est le deep learning au travers d’un exemple et introduire ses concepts clés.
Il est aujourd’hui de plus en plus facile d’avoir accès à de grands ensembles de données, la question qui se pose donc c’est si on peut en retirer de l’information ? Le machine learning est une technique d’apprentissage automatisé. Cela permet à l’ordinateur de « décider » sans avoir été explicitement programmé pour faire des choix. En fait on utilise tous les jours des applications du machine learning sans même le savoir. Par exemple nos emails sont triés en « spam » ou « non-spam » automatiquement, la façon de trier les messages a été apprise basée sur l’ensemble des emails reçus par le provider (Google par exemple) et en utilisant les signalements des utilisateurs. Le deep learning est une des techniques que l’on peut utiliser pour arriver à ce type de résultat, comme nous allons le voir dans cet article. 
Un niveau lycée en maths est conseillé. Il est préférable d’avoir déjà programmé un peu (peu importe le langage) pour comprendre les scripts python. N’hésitez pas à regarder les sources pour aller plus loin !
Mais du coup c'est quoi ?
Le deep learning est une technique de machine learning qui permet de résoudre des problèmes en utilisant un grand niveau d’abstraction.
Mais qu’est-ce que le machine learning ? En fait c’est un ensemble de techniques qui permettent à partir de données de faire apprendre automatiquement à un ordinateur la solution.
Les problèmes les plus classiques sont les problèmes de classification ou de régression :
- Un problème de classification c’est lorsqu’on veut trouver ce que représente une image : est-ce que c’est un chat ou un oiseau ?
- Ce qui est différent d’un problème de régression où on voudrait par exemple trouver le prix d’une maison en fonction de son environnement.
Ok, mais du coup le deep learning en particulier c’est quoi ?
L’idée consiste à utiliser plusieurs couches de neurones afin de laisser la machine apprendre des formes contenues dans nos données.
C’est une technique inspirée par la biologie qui propose un algorithme pour résoudre les problèmes en donnant nos données brutes à l’ordinateur qui se charge tout seul de les découper en sous problèmes et d’apprendre à résoudre ces problèmes tout seul à partir d’exemples.
Mais c’est pour résoudre quels problèmes ?
Le deep learning fonctionne très bien pour des données "continues" comme des images, du son.
Avec les techniques classiques comme les arbres de décisions par exemple, on a besoin de choisir les paramètres qui représentent notre problème.
Par exemple si on souhaite prédire si quelqu’un a survécut sur le Titanic, cela va dépendre de son âge, son sexe, sa cabine, etc. Il y a donc un travail spécifique à faire sur chaque problème pour sélectionner les features. Avec le deep learning en théorie, il n’y a plus besoin de faire ce travail puisqu’on pourrait créer un réseau de neurones capable d’apprendre directement à partir des données de bases.
Quelques exemples concrets ? On peut s’en servir pour
- reconnaitre des images https://research.googleblog.com/2014/09/building-deeper-understanding-of-images.html ;
- reconnaitre du texte, le traduire ou générer du texte similaire ;
- battre le champion du monde de Go ;
- aider au diagnostique médical ;
- en robotique ;
- etc.
C’est une nouvelle technique ?
En fait non ! Une partie de la théorie existe déjà depuis les années 80-90 mais seulement récemment (2012) que la technique a vraiment émergée. On peut donner une petite frise chronologique :
- Années 50 : Les réseaux de neurones sont inventés pour tenter de modéliser comment le cerveau humain fonctionne.
- Années 70 : Il a fallu 20 ans pour découvrir comment faire apprendre le modèle efficacement grâce un algorithme appelé backpropagation.
- Années 90 : Yann Lecun invente les réseaux neuronaux convolutifs. Le problème est qu’à cette époque-là les ordinateurs étaient trop lents pour pouvoir utiliser cette technique en partie et elle est donc oubliée pendant 20 ans
Pas totalement abandonné bien sûr, quelques chercheurs continuent de travailler sur ces techniques mais sans grande considération ni application. - 2012 : Lors d’une compétition internationale (ImageNet) de reconnaissance d’images, les réseaux de neurones sont utilisés et donnent de très bons résultats.
De ce fait les bibliothèques utilisées aujourd’hui sont très jeunes et en plein développement, dans cet article on va utiliser tensorflow afin de réaliser un exemple.
Cette technique a vraiment explosée ces dernières années grâce au ensemble de données qui sont à présent suffisamment grands pour permettre un apprentissage efficace. Également ces calculs sont très efficaces sur les GPU des cartes graphiques, jusqu’à 25 fois plus rapide ! Ce qui permet d’obtenir de temps de calculs qui sont à présent raisonnables.
Problème à résoudre
OK, maintenant on sait à quoi pourrait servir le deep learning, il nous reste à voir comment créer en pratique un réseau de neurones. Dans cet article on va résoudre le problème qui consiste à reconnaitre des chiffres à partir d’images. 
C’est un problème vraiment classique en deep learning et difficile à résoudre sans.
Nos données sont donc des images en noir et blanc et taille 28 par 28 pixels.
Ce problème est très utile en pratique par exemple quand on donne un chèque à sa banque, le chèque est scanné et le montant est reconnu par ce type d’algorithme. Il faut bien entendu commencer par séparer les chiffres ce qui n’est pas fait ici, mais il faut commencer petit.
Comment saura-t-on si notre implémentation est correcte ?
On va utiliser une partie des données pour apprendre (60 000 à 70 000) et le reste (10 000) pour vérifier si notre algorithme est correct. Si une image est un 7 et qu’on prédit un 7 on a raison, si on prédit autre chose c’est faux. Cela nous donne à la fin un score qui est le nombre de chiffres correctement reconnu sur le nombre de chiffres à tester. Pour pouvoir comparer entre algorithme, on va exprime en pourcentage ce résultat.
Il est important de remarquer qu’on ne va pas apprendre sur les données qui servent à tester. En effet, il est possible d’avoir un très bon score sur les données d’entrainement et un mauvais sur d’autres données. Il est donc très important de tester avec des données différentes des données d’entrainement. Ce phénomène est appelé overfitting.
Quel score peut-on espérer obtenir ?
On peut assez facilement obtenir un score proche de 90 %, donc classifier correctement 9 images sur 10. Sur ce dataset, le record est de 99,8 %. 
Réseau de neurones
À présent on sait ce qu’on veut faire, il reste à expliquer le plus important : comment fonctionne un réseau de neurones. Je vais uniquement expliquer comment fonctionne un réseau non convolutif sans quoi ce serait trop compliqué pour une première approche.
Commençons par un neurone
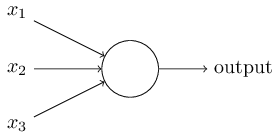
Un peu comme en biologie, un neurone va simplement être une « boite » qui va prendre des informations en entrée et va envoyer un signal en sortie.
On peut voir un neurone comme un réseau de neurone minimal chaque neurone va utiliser les données en entrée et renvoyer une sortie en fonction de ces dernières.
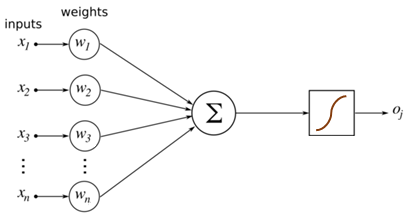
Pour chaque entrée $x_i$, une fois notre neurone « entrainé » on a un poids $w_i$ et un biais $b_i$. Cela va nous permettre de prédire une information de sortie. Imaginons qu’on soit en dimension 2 pour plus de simplicité, on veut séparer des données par une droite comme ci-dessous.
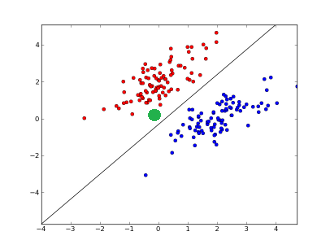
Une fois cette droite trouvée, pour savoir si nos données sont rouges ou bleues il suffit de regarder si on est au-dessus ou en dessous de la droite. On calcule donc $o(x,y) = y - (x-5) = -x + y + 5$ et si le résultat est positif on dit qu’on est rouge sinon bleu. Si on veut savoir si point vert (le point $(0,0)$) devrait être bleu ou rouge, on calcule $o(0,0) = 5$ donc $(0,0)$ serait rouge.
On voit que grâce à cette droite on peut classifier les données en 2 groupes en regardant le signe de la fonction dite d’activation $o$.
Si on résume notre neurone comprends plusieurs éléments :
- Un nombre avec lequel on doit multiplier les entrées : -1 pour $x$, 1 pour $y$. On l’appelle le poids ;
- Un biais que l’on doit ajouter à la fin de l’addition des entrées: 5 ;
- une règle dite d’activation pour classifier les éléments et en déduire la sortie : ≥ 0 rouge, ≤ 0 bleu.
La question qui se pose c’est comment trouver cette droite, mais si vous n’avez pas les concepts mathématiques, il suffit de savoir que c’est un problème d’optimisation et qu’il existe de nombreux algorithmes pour cela.
Le réseau de neurones
Donc si on résume un neurone est un élément qu’on va « entrainer » via les données d’entrée et qui va apprendre des poids et un biais. Si jamais nos données sont séparables comme les données bleues/rouges de l’exemple d’avant alors un neurone suffit à résoudre notre problème mais dans le cas de nos chiffres il semble difficile d’imaginer que ce soit suffisant.
La solution ? En combiner beaucoup. Et si au lieu d’un neurone on en mettait 100 ? 1000 ? On voit qu’il va falloir apprendre 1000 fois des poids, des biais. Du coup plus on a de données, mieux ce sera pour trouver des valeurs correctes afin avoir un bon score de validation.
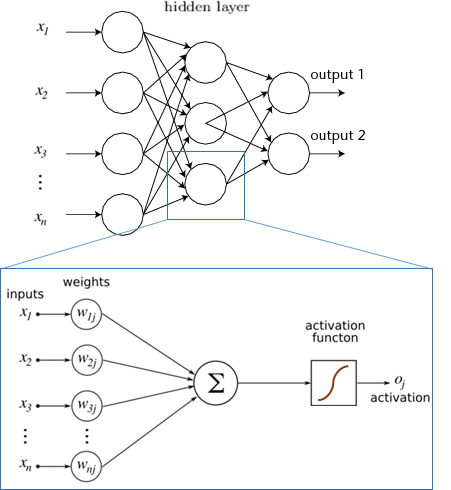
Et non seulement on va mettre beaucoup de neurones mais en plus on va mettre plusieurs couches de neurones où chaque couche va prendre en entrées les sorties de la couche d’avant. On veut vraiment imiter la structure biologique ici. Cela va nous permettre d’apprendre beaucoup plus de formes et de relations entre les données et de permettre à l’ordinateur de gagner en précision.
On peut donner une intuition visuelle dans le cas d’un réseau de neurones qui sert à reconnaitre des visages. Chaque couche du réseau contient une représentation abstraite des données. Comme le cerveau humain on voit que le réseau a construit des couches qui reconnaissent le visage par étape : la forme générale, des parties (nez, oreilles), etc.
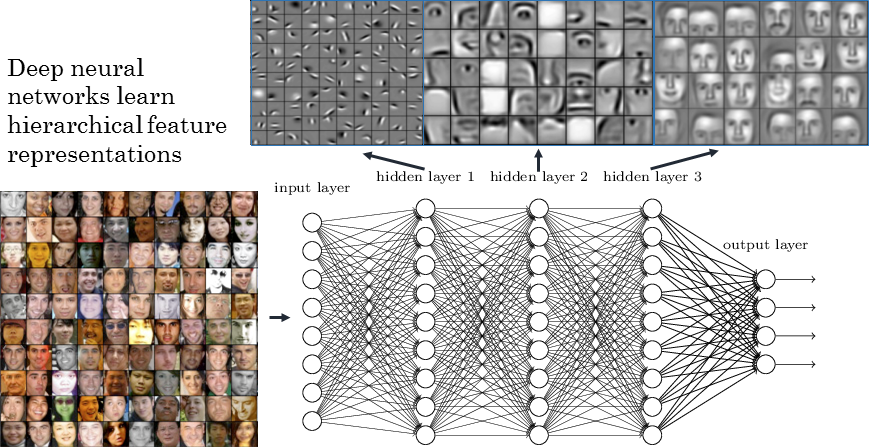
Ce qui est donc également très intéressant c’est que les réseaux de neurones peuvent nous donner accès à des sous représentations des données auxquelles on n’aurait pas forcément pensé ou alors confirmer que l’intuition qu’on a est correcte. Cependant ce n’est pas magique et parfois il est bien difficile de déduire quoi que ce soit comme pour la première couche du réseau ci-dessus.
Un peu de pratique ^_^
Vous avez à présent une idée de ce qu’est un réseau de neurones, on va donc essayer de résoudre le problème du classement des chiffres !
On va utiliser la bibliothèque tensorflow et keras pour cela, et on va coder en python. Même si vous ne connaissez pas python cela aucune importance le code sera très générique et n’utilisera pas de syntaxe spécifique. Le python est très populaire en machine learning pour tester des idées, d’autres préfèrent R mais finalement on peut faire la même chose dans les deux.
Vous pouvez trouver le code ci-dessous sur github.
Keras permet d’avoir une surcouche sur tensorflow qui est déjà haut niveau donc on va écrire un minimum de ligne. C’est bien mais évidemment ça cache complètement ce qui se passe derrière !
Je ne vais pas détailler comment installer python, tensorflow et keras pour ne pas faire un article trop long. Si vous n’avez pas déjà python 3.5 installé sur votre machine, je vous conseille d’utiliser Anaconda pour créer un environnement python 3.5 et ensuite d’installer tensorflow et finalement un pip install keras pour keras.
Commençons par charger notre ensemble de données.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | %matplotlib inline import matplotlib.pyplot as plt import numpy as np from keras.datasets import mnist from keras.models import Sequential from keras.layers.core import Dense, Activation from keras.optimizers import SGD from keras.utils import np_utils nb_classes = 10 #On doit reconnaitre 10 chiffres différents (training_images, training_labels), (test_images, test_labels) = mnist.load_data() print ('Apprentissage : ', training_images.shape[0]) print ('Test : ', test_images.shape[0]) |
Cela nous affiche la taille de nos données (60 000, 10 000) comme décrit dans la partie 2.
On va ensuite afficher quelques exemples histoire d’être sûr que nos données sont correctement chargées.
1 2 3 4 | for i in range(6): plt.subplot(2,3,i+1) plt.imshow(training_images[i], cmap='gray', interpolation='none') plt.title("Chiffre : {}".format(training_labels[i])) |
OK, à présent il faut faire une étape un peu plus technique qui consiste à convertir nos images qui sont sous formes de tableaux 28 par 28 en un vecteur (une colonne) de longueur 784 pour que keras puisse travailler avec. On va aussi diviser les valeurs par 255 pour que notre vecteur ne contienne que des données entre 0 et 1. Finalement on va convertir en catégories les classes de chiffres.
Cette étape est souvent présente en machine learning, il faut souvent reformater ses données pour que les librairies puissent les utiliser.
1 2 3 4 5 6 7 8 9 | training_images = training_images.reshape(60000, 784) test_images = test_images.reshape(10000, 784) training_images = training_images.astype('float32') test_images = test_images.astype('float32') training_images /= 255 test_images /= 255 training_labels_categories = np_utils.to_categorical(training_labels, nb_classes) test_labels_categories = np_utils.to_categorical(test_labels, nb_classes) |
À présent il reste l’étape intéressante ! Le réseau de neurone à proprement parler.
J’ai décidé de créer un réseau qui prend nos entrées, utilise une première couche de 500 neurones et qui ensuite envoie cela dans une couche finale de 10 neurones qui contiendront la probabilité que nos chiffres soit un 1, un 2, etc.
Il y a d’autres paramètres globaux que j’ai choisi et que vous pouvez changer pour améliorer la précision :
- la fonction d’optimisation :
SGD(Stochastique Gradient Descent) et sa « vitesse d’apprentissage »0.5; - la taille du batch :
500, c’est-à-dire le nombre d’images utilisées pour entrainer le réseau ; - le nombre d’epoch :
1, un epoch correspond à un apprentissage sur toutes les données, plus ce nombre est grand plus on devrait obtenir une bonne précision, mais bien sur plus c’est long.
1 2 3 4 5 6 7 8 9 10 11 12 | model = Sequential() model.add(Dense(500, input_shape=(784,))) model.add(Activation('relu')) model.add(Dense(10)) model.add(Activation('softmax')) model.compile(loss='categorical_crossentropy', optimizer=SGD(0.5), metrics=['accuracy']) history = model.fit(training_images, training_labels_categories, batch_size=500, nb_epoch=1, verbose=1, validation_data=(test_images, test_labels_categories)) score = model.evaluate(test_images, test_labels_categories, verbose=0) print('Score sur le dataset de test:', score[1]*100, "%") |
On obtient comme résultat:
1 2 3 4 | Train on 60000 samples, validate on 10000 samples Epoch 1/1 60000/60000 [==============================] - 4s - loss: 0.4613 - acc: 0.8638 - val_loss: 0.2534 - val_acc: 0.9290 Score sur le dataset de test: 92.9 % |
Ce qui est pas mal pour un premier test. 
Il est facile d’avoir plus en bricolant un peu les paramètres et en rajoutant des couches n’hésitez pas à jouer avec et à partager vos réseaux si vous trouvez des valeurs proches de 99 %. 
Pour finir on va afficher des images prédites correctement et incorrectement ce qui permet de voir visuellement des cas que le réseau de neurones n’a pas réussi à identifier.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | classes_predites = model.predict_classes(test_images) correct_indices = np.nonzero(classes_predites == test_labels)[0] incorrect_indices = np.nonzero(classes_predites != test_labels)[0] plt.figure() for i, correct in enumerate(correct_indices[:3]): plt.subplot(1,3,i+1) plt.imshow(test_images[correct].reshape(28,28), cmap='gray', interpolation='none') plt.title("Predit {}, Chiffre {}".format(classes_predites[correct], test_labels[correct])) plt.figure() for i, incorrect in enumerate(incorrect_indices[:3]): plt.subplot(1,3,i+1) plt.imshow(test_images[incorrect].reshape(28,28), cmap='gray', interpolation='none') plt.title("Predit {}, Chiffre {}".format(classes_predites[incorrect], test_labels[incorrect])) |
Voilà pour ce premier aperçu du deep learning. Je sais que j’ai esquivé pas mal de points pour donner un aperçu. N’hésitez pas à me donner vos retours en commentaire et me dire si jamais vous souhaiter d’autres articles plus approfondis. On pourrait par exemple
- réimplémenter le réseau sans utiliser de bibliothèque pour comprendre/coder nous même un algorithme d’optimisation (descente de gradient stochastique par exemple) et la backpropagation ;
- regarder les réseaux de neurones convolutifs ;
- utiliser le deep learning pour faire des traductions à la Google translate…
Merci beaucoup à Gabbro pour les corrections et la validation de cet article.
Sources et liens pour approfondir
N.B. : quasiment toutes mes sources sont en anglais, je ne connais pas de bonnes sources en français.
- https://github.com/Orpheo298/deep-learning-tutorial/blob/master/deep_learning_tutorial.ipynb le répertoire github avec le notebook utilisé dans cet article ;
- https://github.com/ChristosChristofidis/awesome-deep-learning un bon marque page avec pleiiiin de très bons liens vers des sites/cours/vidéos ;
- https://www.tensorflow.org et https://keras.io/ les frameworks utilisés dans l’article ;
- http://neuralnetworksanddeeplearning.com/ un livre en ligne plutôt didactique sur le deep learning ;
- https://www.kaggle.com/ un site de compétition et de dataset pour le machine learning ;
- http://colah.github.io/posts/2015-08-Backprop/ des explications sur la backpropagation ;
- http://cs.stanford.edu/~quocle/tutorial1.pdf un cours d’introduction sur la backpropagation et les réseaux de neurones ;
- http://www.rsipvision.com/exploring-deep-learning/ la source de l’image du réseau pour la reconnaissance faciale.
